3. 逻辑系统·布尔代数基础[英]

Logical System and Boolean Algebra

Logical System

Logical System is a kind of system based on Boolean Algebra (布尔运算) which can be represented by a black box（黑箱）.
It has a set of input lines.

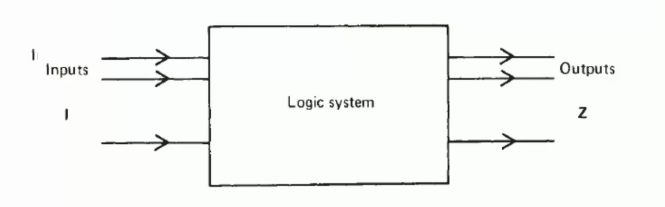
Logic Gate(逻辑门) is a kind of circuit parts which can do the Boolean algebra according to the voltage level.

Parameters of a logical gate:
- Input --\(I\)
- Output --\(Z\)
- Time --\(T\)

A logical system can be expressed as:
\[Z_t=f(I_t)\] where \(Z_t\) is the output and \(I_t\) is the input at time \(t\).

Types of logical system

Combinational Logical System

If \(I\) and \(Z\) always constant, which means the value of Z does not change by time, this kind of logical system called Combinational Logical System (组合逻辑系统).
Same input in different time, the output is the same.
Example: Adder (加法器)

Sequential Logical System

If \(I_t\) and \(Z_t\) vary depending on time, this kind of logical system called Sequential Logical System （时序逻辑系统）.
It has memory.
The value of \(Z\) always vary from time to time.
Same input in different time, the output is different. Because the value depends on current and previous result.
Example: Accumulator（累加器）,whose \(output=input+previous output\).

Combinational Logical System can be converted into Sequential Logical System.

Storage Logical System

Storage Logical System is another logical system designed to hold information. Its input are address information and data information.
The address is corresponding to the data.
It can be organized into a Combinational Logic Function.
Example: Memory(内存)

Logical and Propositional Statements

True or False can be described as Binary format.
For example, True presents for 1 and False presents for 0. Any condition which has 2 cases is able to be described by 1-0 logical statements.
One case is represented by 1, the other is by 0.
The leading result can also be described by logical states.
Example:
To be the winner of 100 meter race(W):
Condition to be a winner: fist one(F) and not foul(O)
Only if F is True and O is True, W is True.
So the condition of winner can be described as \(W=F  AND  O\) or \(W=F.O\).

Truth Table

Truth Table(真值表) is a classical form based on logical statements to describe the relationship between all the possible conditions(inputs) and results(outputs).
In above example, the condition can also be described as a truth table.

F	O	W
T	T	T
T	F	F
F	T	F
F	F	F

Which can be converted to:

F	O	W
1	1	1
1	0	0
0	1	0
0	0	0

In digital system, the voltage can be used to present true(1) or false(0).

Example: Employment
To be employed you must satisfied:
1. Unmarried females under 25 years old
2. Married Male under 25 years old
3. Over 25 year

Attributes in this case:
- Marriage:
Married(\(M\)) Unmarried(\(\overline{M}\))
- Sex:
Female(\(S\)) Male(\(\overline{S}\))
- Over 25 years：
Over(\(A\)) or not(\(\overline{A}\))

Totally, we have \(2^3=8\) cases of inputs.

The condition of employed(\(E\))are：
1. \(\overline{M}.\overline{S}.\overline{A}\)
2. \(M.S.\overline{A}\)
3. \(A\)

If one can satisfy any one above three condition, he can be employed, therefore, the employ condition is concluded as:
\[E=(\overline{M}.\overline{S}.\overline{A})+(M.S.\overline{A})+A\]

The true table can be expressed as:

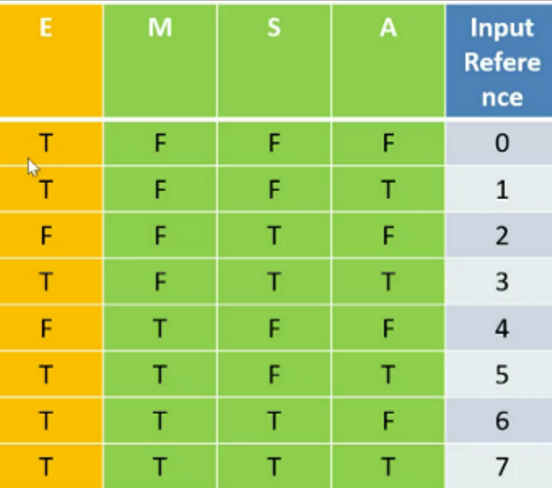
Then we need to construct such a kind of logic system.

Binary connectives

An elementary function of 2 inputs(二元函数).
There are 3 basic connectives :
- OR(+) （或）
Just one of inputs is true , Output is true.
- AND(.)（且）
Both of inputs is true, Output is true.
- NOT(-/')（非） Inverse case of a logical variable.

Besides, EXCLUSIVE-OR is a common logical connective.
- EXCLUSIVE-OR(⊕)（异或）
If 2 Inputs are the same, Output is true.

“N” is represented for the inverse value(1/0) of result.

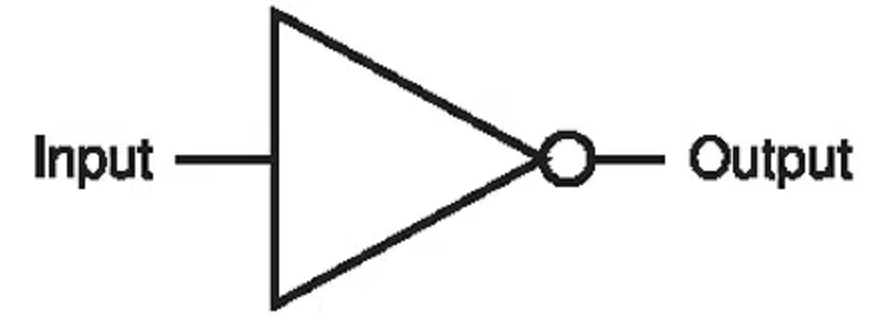
Gate(逻辑门)

Circuit within the systems that carry out the elementary logical operations.
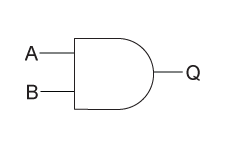
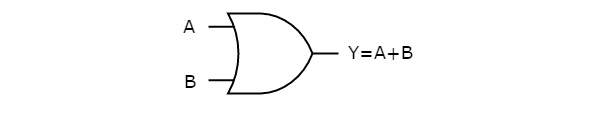
Three fundament gates are:
- AND(\(A.B\))

- OR(\(A+B\))

- NOT(\(\overline{A}\)/\(A'\))

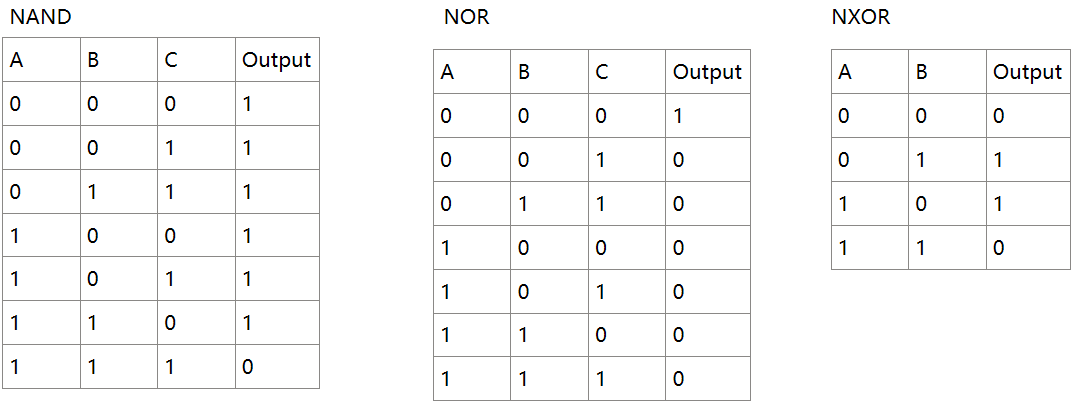
Other logical gates can be implemented by those basic gates: - XOR(\(A.\overline{B}+\overline{A}.B\))
- NAND(\(\overline{A.B}\))
- NOR(\(\overline{A+B}\))
- EQUIV ALENCE(NOT XOR)(\(\overline{A.\overline{B}+\overline{A}.B}\))

The circuit parts of gates name is the combination of gate's kind name and numbers of inputs.
For example, XOR3 stands for XOR gates which has 3 inputs.

Introduction of Boolean Algebra

Boolean Algebra is an algebra system using logical connectives to do calculations.
Venn Diagrams(韦恩图) can help to do the calculation.

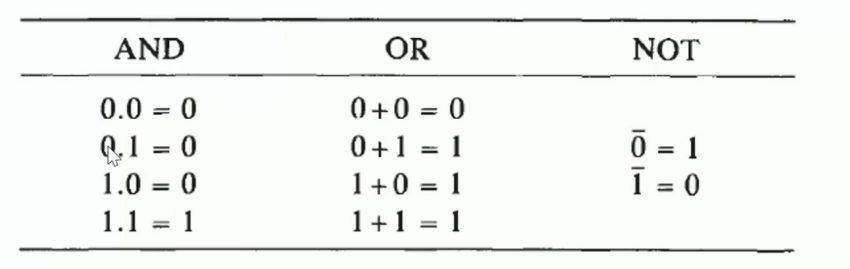
None variable caculation

0 is powerful in AND operation : if there is a 0, the AND result will be 0.
1 dominates OR operation : if there is a 1, the OR result will be 1.

Caculation Order

\[(·)>AND>OR>NOT\] \((·)\) has the highest order.

One variable caculation

AND	OR	NOT
\(A.0=0\)	\(A+0=A\)
\(A.1=A\)	\(A+1=1\)	\(\overline{\overline{A}}=A\)
\(A.A=A\)	\(A+A=A\)
\(A.\overline{A}=0\)	\(A+\overline{A}=1\)

Logical Simplification

To decrease the energy cost and calculation resource, we need to do logical simplification.

Properties of Boolean Algebra

The simplified method is based on the properties of Boolean Algebra.

• Communicative(交换律)
  \[A+B=B+A\] \[A.B=B.A\]

• Absorptive（吸收律）
  \[A+A.B=A\] \[A(A+B)=A\]

• Associative（结合律）
  \[A+(B+C)=(A+B)+C\] \[A.(B.C)=(A.B).C\]

• Distributive（分配律）
  \[A.(B+C)=A.B+A.C\] \[A+(B.C)=(A+B).(A+C)\]

• De Morgan's Theorems(反演定理/德摩根律)
  OR to NAND:
  \[(A+B)'=A'.B'\]
  AND to NOR:
  \[(A.B)'=A'+B'\]

• Minimizatin Theorems \[A.B+A.\overline{B}=A\]

  Proof:
  \[\begin{aligned} A.B+A.\overline{B}&=A(B+\overline{B})\\ &=A(B+\overline{B})\\ &=A.1\\ &=A \end{aligned}\]

  
  \[(A+B)(A+\overline{B})=A\]

  \[\begin{aligned} (A+B)(A+\overline{B})&=A.A+A.\overline{B}+B.A+B.\overline{B}\\ &=A+A.(B+\overline{B})+0\\ &=A \end{aligned}\]

  
  \[A+\overline{A}.B=A+B\] \[A.(\overline{A}+B)=A.B\]

• Duality Principles （对偶定理）
  Mark Inversion(\(A→\overline{A}\) \(AND↔OR\)) of one caculation is possible.
  For example:
  \[F=A+(B.\overline{C})↔\overline{F}=\overline{A}+(\overline{B}.C)\]

Equivalence Proof

There are 4 ways to proof logical equivalence.

1. Truth Table（真值表）

2. Logical Reasoning(逻辑证明)

3. Venn Diagram（韦恩图）

4. Circuit equivalence (等效电路图)

Example: proof \((A+\overline{B}).(\overline{A}+\overline{B}+C)=A.C+\overline{B}\)

\(A\)	\(B\)	\(C\)	\(A+\overline{B}\)	\(\overline{A}+\overline{B}+C\)	\((A+\overline{B}).(\overline{A}+\overline{B}+C)\)	\(A.C+\overline{B}\)
0	0	0	1	1	1	1
0	0	1	1	1	1	1
0	1	1	0	1	0	0
1	1	1	1	1	1	0
1	0	0	1	1	1	1
…	…	…	…	…	…	…